前言
最近在看GCN,大致了解了做GCN的两条路:
- 基于spectral(谱)的方法
- 基于spatial(空域)的方法
其中基于空域的方法更容易理解,因为整个过程比较直观,符合我们正常的思维习惯。但是基于谱的方式就显得非常抽象,它抽象的地方不仅在于傅里叶变换,更在于对图的拉普拉斯算子进行分解这一步。就算你搞清楚了连续函数的傅里叶变换,也很难直接一步到位。
查询了很多资料,我觉得正确的理解顺序应该是:
- 了解卷积和傅里叶变换间的关系
- 了解矩阵和线性算子的特征分解(谱分解)
- 了解连续拉普拉斯算子的谱分解与傅里叶变换的关系
- 了解图拉普拉斯算子(拉普拉斯矩阵)与拉普拉斯-贝拉米算子、连续拉普拉斯算子间的关系
理解顺序图如下所示:
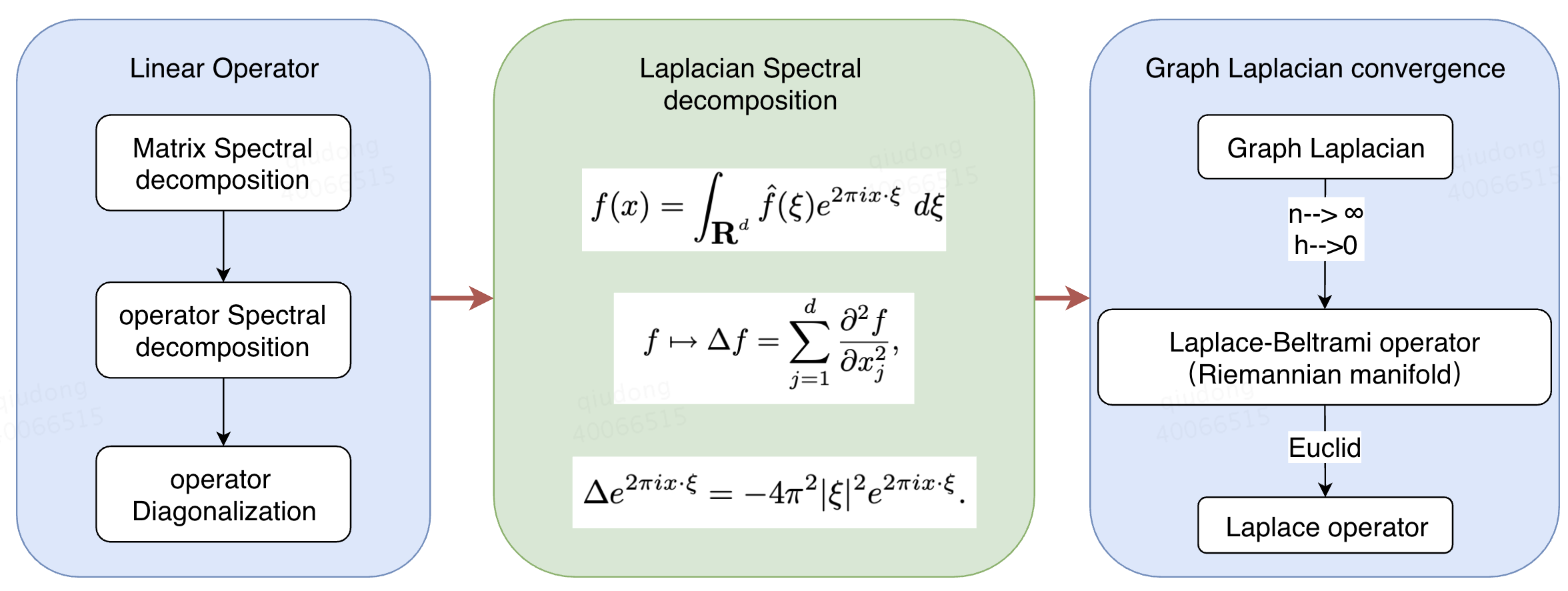
这系列博客目的仅仅在于理清思路,不会涉及详细推导,重要的结论会有相应的论文在附录给出。
核心难点
总的来看,要理解基于拉普拉斯矩阵谱分解进行的图卷积方法,难点在于理解拉普拉斯算子和拉普拉斯矩阵的关系,以及拉普拉斯算子和傅里叶变换的关系。这里面涉及到的线性变换的一些基础理论比如谱定理、线性变换和矩阵的关系等等。如果可以将他们串联起来,对图卷积的理解一定会更上一层楼。
线性映射和矩阵
矩阵和算子
算子(operator)可以理解为一种映射,它将一个线性空间X内的元素a映射为同一个空间内的另一个元素b。这里的重点是同一个空间中,这里同一个可以理解为均为函数空间,或者均为某n维空间。
线性算子(Linear Operator)是一类特殊的算子,它满足以下两个条件:
- 数乘: $T(k\alpha)=kT(\alpha)$
- 加法: $T(\alpha+\beta)=T(\alpha)+T(\beta)$
很显然,一阶微分算子、积分算子都属于线性算子,他们作用的空间叫做函数空间。
矩阵(Matrix)可以视为线性映射的一种表达方式。矩阵是将线性空间V中的元素a映射到另一个线性空间W中的元素b。
- 数乘: $T(k\alpha)=kT(\alpha)$
- 加法: $T(\alpha+\beta)=T(\alpha)+T(\beta)$
如果V与W的维度相同,那么他们属于同一个空间,矩阵此时为n*n的方阵,也称为算子。能用矩阵表达的算子,均作用在有限维空间上(比如二维、三维、n维欧几里得空间),而函数空间是无限维空间,所以微分算子、积分算子等无法用有限维矩阵来表示。
线性空间的基
我们只讨论线性空间(向量空间),线性空间的线性同样也是满足几个基本条件:
向量空间中的元素要满足:
- 数乘: $k(\alpha+\beta)=k\alpha+k\beta$
- 交换律:$\alpha+\beta=\beta+\alpha$
- 结合律:$(\alpha+\beta)+\gamma=\alpha+(\beta+\gamma)$
- …
如果有一个空间,不管里面的元素具体是指什么内容,只要他们满足上述的几个条件,这个空间就叫做线性空间,就可以用线性代数的一切方法进行抽象化的计算。
建立起线性空间后,存在一类特殊的元素集合,用这类元素集合可以唯一表示该空间中所有其他元素,我们称其为空间的基,很显然,一个空间有无穷多组基,如果一组基他们互相正交并且长度为1,我们就称为规范正交基。
现在我们抛开规范正交基,选取空间V的任意一组基$(v_1,v_2,v_3,…,v_n)$,那么空间V中任意一元素$\alpha$可被表示为:
我们定义一个线性映射T,它将基$(v_1,v_2,….,v_n)$映射为新的元素$(T(v_1),T(v_2)…,T(v_n))$,然后新的元素同样用基$(v_1,v_2,….,v_n)$表示:
那么,我们可以将映射后的元素$T(\alpha)$表示为
展开合并后得到:
仔细考察整个过程,我们把基变换的表示写成”矩阵”,把$\alpha$写成”向量”:
是不是有内味了,我们可以说,矩阵M(T)其实是一种记录方式,它用这种方式记录了一组基的变换情况,元素$\alpha$其实是跟随着基的变化而变换的。因此矩阵M(T)记录着关于基变换的信息。
下面用一个图展示下基变换的意义: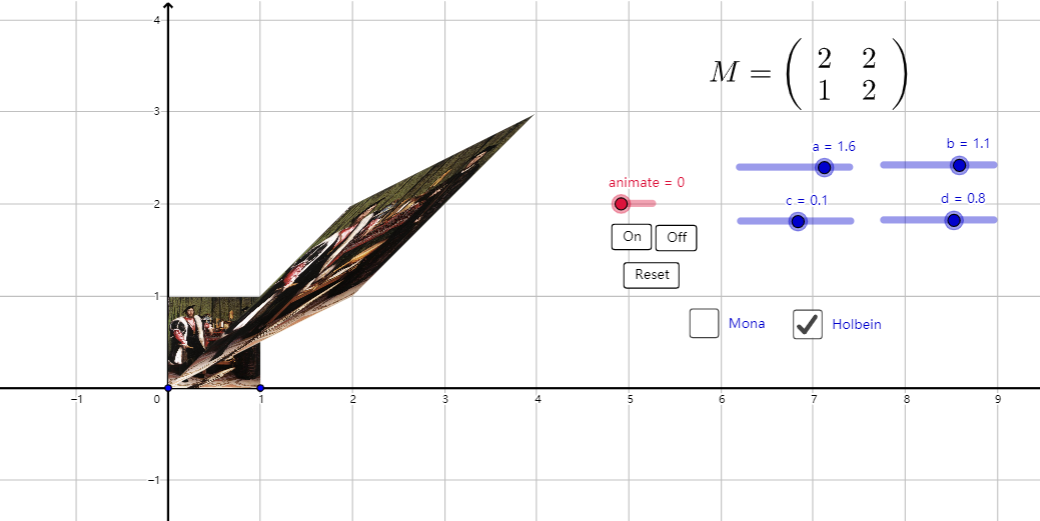
图片的纵横两个边表示原始的基,图片的右上角点跟随着基的变化而变化。
关于矩阵的理解角度有很多种,这只是其中一种。
要注意的是,线性变换T一旦确定,就是固定不变的,T是我们定义好的映射,它只与初始定义有关,而T的矩阵M(T),其实与选择的基密切相关,矩阵完整的写法为$M(T,(v_1…v_n),(w_1…w_m))$,就是说,T的矩阵形式,与源空间V的基有关,也与目标空间W的基有关,只不过当V与W的维度相同的时候,我们将其视为一个空间,共用一个基进行表示,并且在不特殊说明的情况下,我们默认这个基是标准正交基,也可以省略。
总结一下,线性映射T是固定的,它的矩阵形式M(T)与选择的基密切相关,选择不同的基,线性映射有不同的矩阵形式,只不过在绝大多数情况下,默认使用标准正交基,也就省略了说明,下一节关于特征向量和特征值我们有更直观的例子。
特征向量和特征值
定义矩阵算子之后,我们可以考察在线性映射过程中一类特殊的元素。对于空间V,有一个线性映射T,它将元素$\alpha$映射到V的另一个元素$\beta$,但是有一类特殊的元素$(u_1,u_2,…,u_n)$,他们在这个线性变换前后,”方向”不变,只改变”大小”:
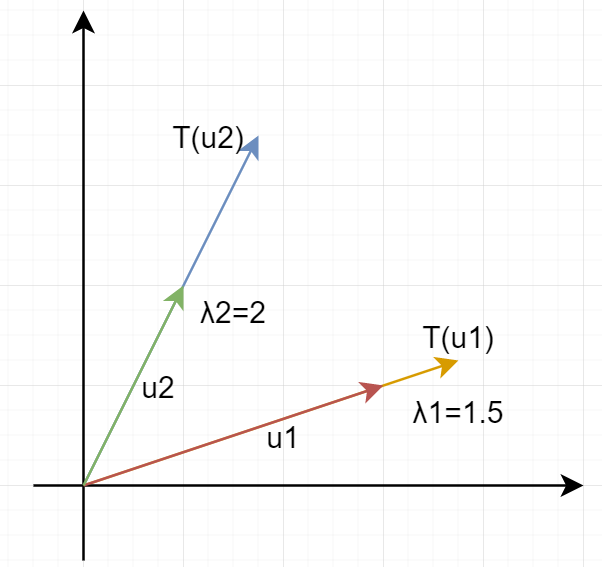
为什么叫做”特征”向量,或者”本征”向量,是因为这些特殊的向量完全反映了这个线性变换T的内在本质。
特殊向量又叫不变子空间,例如由特征向量$u_1$构成的一维线性空间中的元素,全部都是不改变方向的,他们都是特征向量,并且这个子空间的元素都会被拉长$\lambda_k$倍。因此特征向量重要的是表示了一个不变的“方向”,特征值表示了对应方向的拉伸比例。
这些不变的子空间并不是反映矩阵的本质,而是线性变换T的本质。上一节我们说到过,T在不同的基下面,会有不同的矩阵形式,假如我们用不变子空间、也就是特征向量作为基(如果特征值数量与维度相同且特征向量不共线),M(T)是什么样的?沿袭上一节的写法,我们取T的特征向量作为空间V的一组基$(u_1,u_2,…,u_n)$,那么空间中任意一元素$\alpha$可被表示为:
如图所示: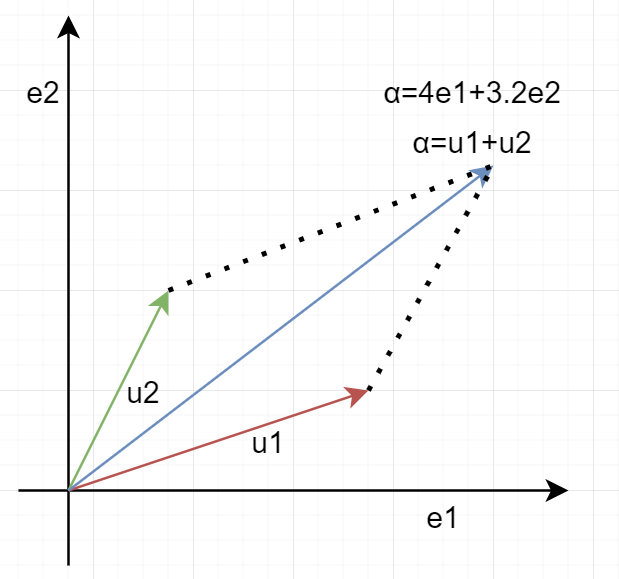
对其进行线性变换:
如图所示: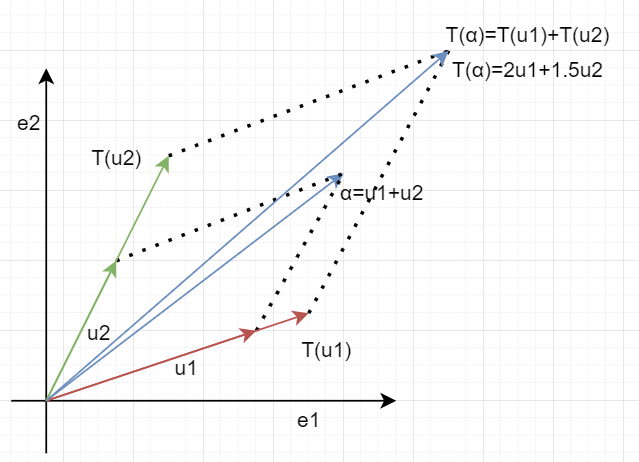
同样的,我们把基变换写出:
那么,T关于基$(u_1,…,u_n)$的矩阵就是:
有内味了,T关于不同的基有不同形式的矩阵,最特殊的,最简单的就是这一种对角矩阵。它表示,如果你是用T的特征向量作为基表示其他元素,经过线性变换T后,对应元素的每个维度相应的被拉伸了$\lambda_k$倍。这叫做矩阵对角化。
谱定理
上一节谈到了矩阵对角化,我们用更形式化的符号推导,设P是由T的特征向量按列排列组成的矩阵:
假如P可逆:
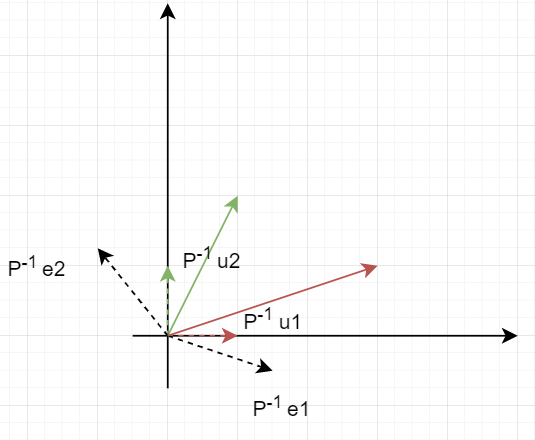
$T=P\Lambda P^{-1}$ 实际反映了一个简单的事实,将线性变换T作用在元素$\alpha$上,可以分解为三步线性变换:
$P^{-1}$算子将每一个特征向量变换到对应的标准正交基。原来的标准正交基变到某一个位置:
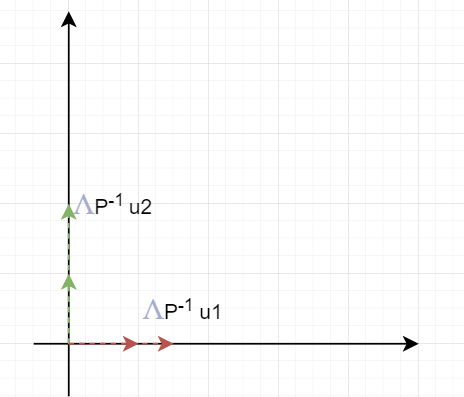
经过上一步变换,特征向量已经变到标准正交基了,此时空间内所有向量的坐标都是用标准正交基的来表示,可以说,此时的坐标就是在特征向量作为基下的坐标。 然后将标准正交基拉伸$\Lambda$倍。
- 最后将标准正交基通过$P$再变回到特征向量的位置。
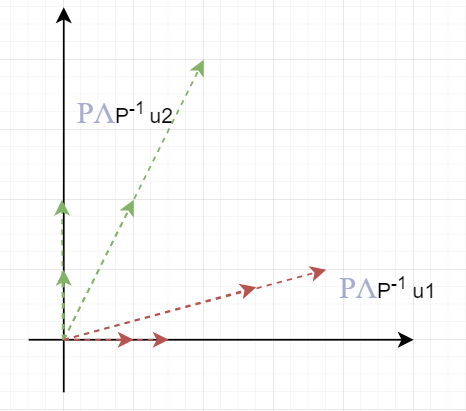
元素$\alpha$在三步中随着基的变化而变化即可。
更特殊的是,如果T的特征向量恰好是V的一组规范正交基(互相正交且模为1,注意区别标准正交基),也就是P是酉矩阵(这种矩阵只旋转元素,不改变大小),那么这种T我们认为它是空间V上最好的算子,因为它的形式最简洁,性质最好研究。那么满足什么条件的线性映射才有这种好的性质呢?这就是谱定理研究的内容:
当且仅当$T=T^{*}$,那么T的特征向量可以组成V的一组规范正交基。我们满足这个条件的算子T为V上的自伴算子。
因为满足谱定理的矩阵必定可以对角化,因此我们可以称矩阵对角化为特征分解或谱分解。下一章详细讨论函数空间内拉普拉斯算子的谱分解。